Photo

10 notes
·
View notes
Photo

New ξ just dropped.
9 notes
·
View notes
Video
youtube
2 notes
·
View notes
Photo
The story continues.
150 notes
·
View notes
Text
I disagree.
Let (G, Δ, ε) be a comonoid object in a (cartesian) monoidal category (C, ×, 1). It then follows from the counitality diagram that the composites
π₁ ∘ Δ , π₂ ∘ Δ : G → G
are both the identity morphism of G. The morphism
Δ : G → G × G
is therefore the diagonal morphism.
There hence exists one, and only one, comonoid structure on every object of C. (This is also what https://ncatlab.org/nlab/show/comonoid states.) This comonoid structure is given by the diagonal morphism Δ : G → G × G and the unique morphism ε : G → 1.
Anyway, all this work was motivated by the fact that apparently given two commuting idempotent endomorphisms L and R of a group G, the homomorphism Δ : G -> G×G, g ↦ (L(g), R(g)) describes a comonoid object in (Grp, ×, {1})
I wonder what happens with the monoidal structure given by the free product (Grp, *, {1})
*loses another three hours*
4 notes
·
View notes
Photo
The previous post made me remember this classic.

150 notes
·
View notes
Photo

150 notes
·
View notes
Text
Given any two groups G and H we can consider their product
P = G × H.
Both “internal projections”
p : P → P, (g, h) ↦ (g, 1)
and
q : P → P, (g, h) ↦ (1, h)
are group endomorphismn. Both of them are idempotent, and they commute.
Whoever can find a pair of commuting, idempotent endomorphisms L, R of a group* wins a cookie (and a Comonoid object in the category of groups)
mmmh after thinking about it more it seems like we must have L = R after all, what a bummer :(
*non abelian please
13 notes
·
View notes
Text
Where × = ⊗.
I need a name for a 'semiring-but-it-doesn't-necessarily-have-0-or-1', so what do y'all think of 'distributive bialgebra'.
19 notes
·
View notes
Text
Hopefully you can just undo your editors replace action.
You could also try to improve the damage done by enabling autosave and having the editor crash while trying to fix the problem. (If the editor refuses to crash, then you can also accidently close it.)
LaTeX disaster speedrun
Just hit a replace command "\P -> \PP" on my latex editor (texmaker), I made the mistake of not selecting the text I wanted to replace so it acted on the whole document which is a bad thing by itself I guess
BUT ALSO said editor by default doesn't check for capitalization (you have to manually check this setting) so now all my \pi are now \PPi, all my \prod are now \PProd, my \phi are \PPhi and so on
MOREOVER I just now found out i had already defined another command \PPP so now I have a hellscape of \PP, \PPPP and \PPPPP scattered all across number theory exercises
4 notes
·
View notes
Text
Yes, if h is central in g then the argument works. It sufficies more generally that h is “relatively” nilpotent in g in the sense that the decreasing sequence
h, [g, h], [g, [g, h]], [g, [g, [g, h]]], …
eventually reaches zero. (†)
I like to think about this in term of representations:
If M is a representation of a Lie algebra g, then we can consider its suprepresentation gM, which is spanned (as a vector space) by all elements xm with x in g and m in M. We say that the representation M is nilpotent, or that g acts nilpotently on M, if the decreasing sequence
M, gM, g(gM), g(g(gM)), …
eventually reaches zero.
We then have the following:
• The Lie algebra g is nilpotent if and only if its adjoint representation is nilpotent.
• An ideal h of g in relatively nilpotent (in the above sense) if and only if the adjoint action of g on h is nilpotent.
• If h is an ideal of g and M is a representation of the quotient Lie algebra g/h, then we can regard M as a representation of g, and have (g/h)M = gM.
Your original “proof” can be modified to give the following observation:
Proposition. Let g be a Lie algebra, let M be a representation of g and let N be a subrepresentation of M. The representation M is nilpotent if and of if both the subrepresentation N and the quotient representation M/N are nilpotent.
The above proposition and three statements give (†). The key point here is that everything is done relative to the fixed Lie algebra g.
[7/?] Today I sent the talk slides to the lecturer and he said they were very good! So I can stop worrying about that and focus on the rest of the exam. Two days to revise all the exercises again and the theory (although I know we won’t be asked to know every theorem by heart like in some other exams).
Here’s a very quick/bad proof of a fact that I always struggle to remember:
Thm. Let g be a Lie algebra and h < g be an ideal. If both h and g/h are nilpotent then so is g.
Proof. A commutator of length m is an expression of the form [a1, [a2, … , [am-1, am]]]. Since the projection g -> g/h onto the quotient is a Lie algebra morphism, commutators in the quotient corresponds to commutators in g. The fact that g/h is nilpotent means that for some k > 0 all commutators in g/h of length > k are null, but this means that all commutators in g of length > k belong to h. This in turn means that for all m > k the m-th derived ideal of g belongs to the m-th derived ideal of h, but since h is nilpotent these are eventually (for some m’ > 0) the trivial ideal, and so g is nilpotent too. \qed
8 notes
·
View notes
Text
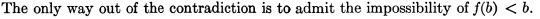
This time from Halmos.
ways to end proofs
QED
which was what we wanted (abbreviated w⁵, or u¹⁰, or even v¹⁰)
■ (or □ for lemmas)
♥
So there.
The rest is obvious.
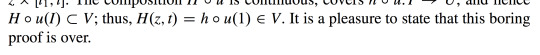
2K notes
·
View notes
Text
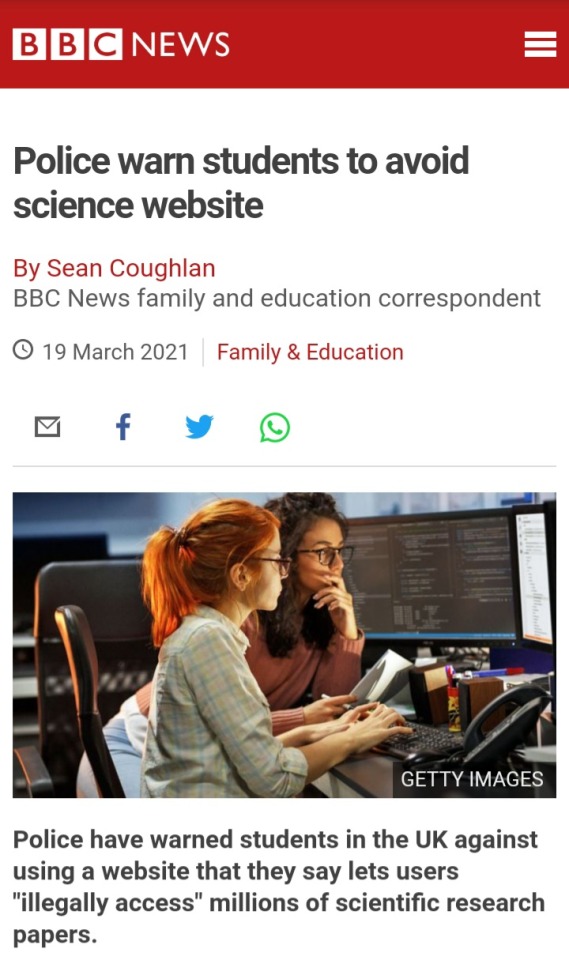
This is about Sci-Hub. yeah we get it.. gatekeep knowledge and protect the interests of capital…
271K notes
·
View notes
Text
This “theorem” is wrong.
Example. Let g be the two-dimensional Lie algebra with basis x, y and Lie bracket [x, y] = y. The one-dimensional linear subspace h of g spanned by y is an ideal of g. Both h and g/h are one-dimensional and thus nilpotent. But g is not nilpotent.
Exercise. Find the mistake in the above “proof”.
[7/?] Today I sent the talk slides to the lecturer and he said they were very good! So I can stop worrying about that and focus on the rest of the exam. Two days to revise all the exercises again and the theory (although I know we won’t be asked to know every theorem by heart like in some other exams).
Here’s a very quick/bad proof of a fact that I always struggle to remember:
Thm. Let g be a Lie algebra and h < g be an ideal. If both h and g/h are nilpotent then so is g.
Proof. A commutator of length m is an expression of the form [a1, [a2, … , [am-1, am]]]. Since the projection g -> g/h onto the quotient is a Lie algebra morphism, commutators in the quotient corresponds to commutators in g. The fact that g/h is nilpotent means that for some k > 0 all commutators in g/h of length > k are null, but this means that all commutators in g of length > k belong to h. This in turn means that for all m > k the m-th derived ideal of g belongs to the m-th derived ideal of h, but since h is nilpotent these are eventually (for some m’ > 0) the trivial ideal, and so g is nilpotent too. \qed
#math#lie algebras#is the proof “bad” because it is wrong?#was this meant to be a joke?#this would make me look stupid#am I overthinking this?
8 notes
·
View notes
Text
???
How is this site still alive?!
2 notes
·
View notes
Photo
The two genders
6 notes
·
View notes
Text
Homotopy is the pumpkin spice of mathematics.
63 notes
·
View notes